Understanding Residual Networks
Probably about residuals, right?
We've covered the basics of CNNs with the MNIST data set where we trained a model to recognize handwritten digits. Today, we'll be moving towards residual networks that allow us to train CNNs with more layers.
Since we've already got a good result with the MNIST data set, we'll move onto the Imagenette data set, which is a smaller version of the ImageNet data set.
We train with a smaller version so that we can make small changes without having to wait long periods of time for the model to train.
def get_dls(url, presize, resize):
path = untar_data(url)
return DataBlock((ImageBlock, CategoryBlock), get_items=get_image_files,
splitter=GrandparentSplitter(valid_name='val'),
get_y=parent_label, item_tfms=Resize(presize),
batch_tfms=[*aug_transforms(min_scale=0.5, size=resize),
Normalize.from_stats(*imagenet_stats)]
).dataloaders(path, bs=128)
dls = get_dls(URLs.IMAGENETTE_160, 160, 128)
dls.show_batch(max_n=4)
First, we'll first change how our model works. With the MNIST data set, we have images of shape 28 $\times$ 28. If we added a few more layers with a stride of 1, then we'd get more layers. But, how do we do classification for images with sizes that aren't 28 $\times$ 28? And, what do we do if we want to have additional layers of different strides?
In reducing the last two dimensions of our output from each layer (the height and width) through strides, we get two problems:
- with larger images, we need a lot more stride 2 layers; and
- the model won't work for images of different shape than our training images.
The latter can be solved through resizing, but do we really want to resize images to 28 $\times$ 28? We might be losing a lot of information for more complex tasks.
So, we solve it through fully convolutional networks, which uses a trick of taking the average of activations along a convolutional grid. In other words, we take the average of the last two axes from the final layer like so:
def avg_pool(x):
return x.mean((2, 3))
Remember that our final layer has a shape of n_batches * n_channels * height * width. So, taking the average of the last two axes gives us a new tensor of shape n_batches * n_channels * 1 from which we flatten to get n_batches * n_channels.
Unlike our last approach of striding until our last two axes are 1 $\times$ 1, we can have a final layer with any value for our last two axes and still end up with 1 $\times$ 1 after average pooling. In other words, through average pooling, we can have a CNN that can have as many layers as we want, with images of any shape during inference.
Overall, a fully convolutional network has a number of convolutional layers that can be of any stride, an adaptive average pooling layer, a flatten layer, and then a linear layer. An adaptive average pooling layer allows us to specify the shape of the output, but we want one value so we pass in 1:
def block(ni, nf):
return ConvLayer(ni, nf, stride=2)
def get_model():
return nn.Sequential(
block(3, 16),
block(16, 32),
block(32, 64),
block(64, 128),
block(128, 256),
nn.AdaptiveAvgPool2d(1),
Flatten(),
nn.Linear(256, dls.c)
)
The ConvLayer is fastai's version of our conv layer from the last blog, which includes the convolutional layer, the activation function, and batch normalization, but also adds more functionalities.
Activation function or nonlinearity? In the last blog, I defined ReLU as a nonlinearity, because it is a nonlinearity. However, it can also be called an activation function since it's taking the activations from the convolutional layer to output new activations. An activation function is just that: a function between two linear layers.
In retrospect, our simple CNN for the MNIST data set looked something like this:
def get_simple_cnn():
return nn.Sequential(
block(3, 16),
block(16, 32),
block(32, 64),
block(64, 128),
block(128, 10),
Flatten()
)
In a fully convolutional network we have what we had before in a CNN, except that we pool the last two axes from our final convolutional layer into a unit axis, flatten the output to get rid of the unit axis, then use a linear layer to get dls.c output channels. dls.c returns how many unique labels there are for our data set.
So, why didn't we just use fully convolutional networks from the beginning? Well, fully convolutional networks take an image, cut them into pieces, shake them all about, do the hokey pokey, and decide, on average, what the image should be classified as. However, we were dealing with an optical character recognition (OCR) problem. With OCR, it doesn't make sense to cut a character into pieces and decide, on averge, what character it is.
That doesn't mean fully convolutional networks are useless; they're bad for OCR problems, but they're good for problems where the objects-to-be-classified don't have a specific orientation or size.
Let's try training a fully convolutional network on the Imagenette data set:
def get_learner(model):
return Learner(dls, model, loss_func=nn.CrossEntropyLoss(),
metrics=accuracy).to_fp16()
learn = get_learner(get_model())
learn.fit_one_cycle(5, 3e-3)
Now we're ready to add more layers through a fully convolutional network. But, how does it turn out if we just add more layers? Not that promising.

You'd expect a model with more layers to have an easier time predicting the correct label. However, the founders of resnet found different results when training and comparing the results of a 20- and 56-layer CNN: the 56-layer model was doing worse than the 20-layer model in both training and test sets. Interestingly, the lower performance isn't caused by overfitting because the same pattern persists between the training and test errors.
However, shouldn't we be able to add 36 identity layers (that output the same activations) to the 20-layer model to achieve a 56-layer model that has the same results as the 20-layer model? For some reason, SGD isn't able to find that kind of model.
So, here comes residuals. Instead of each layer being the output of F(x) where F is a layer and x is the input, what if we had x + F(x)? In essense, we want each layer to learn well. We could go straight to H(x), but we can have it learn H(x) by learning F(x) = H(x) - x, which turns out to H(x) = x + F(x).
Returning to the idea of identity layers, F contains a batchnorm which performs $\gamma y + \beta$ with the output y. We could have $\gamma$ equal to 0, which turns x + F(x) to x + 0, which is equivalent to x.
Therefore, we could start with a good 20-layer model, initialize 36 layers on top of it with $\gamma$ initialized to 0, then fine-tune the entire model.
However, instead of starting with a trained model, we have something like this:
In a residual network layer, we have an input x that passes through two convolutional layers f and g, where F(x) = g(f(x)). The right arrow is the identity branch or skip connection that gives us the identity part of the equation: x + F(x), whereby F(x) is the residual.
So instead of adding on these resnet layers to a 20-layer model, we just initialize a model with these layers. Then, we initialize them randomly per usual and train them with SGD. Skip connections enable SGD to optimize the model even though there's more layers.
Why resnet works so well compared to just adding more layers is like how weight decay works so well: we're training to minimize residuals.
At each layer of a residual network, we're training the residuals given by the function F since that's the only part with trainable parameters; however, the output of each layer is x + F(x). So, if the desired output is H(x) where H(x) = x + F(x), we're asking the model to predict the residual F(x) = H(x) - x, which is the difference between the desired output and the given input. Therefore at each optimization step, we're minimizing the error (residual). Hence a residual network is good at learning the difference between doing nothing and doing something (by going through the two weight layers).
So, a residual network block looks like this:
class ResBlock(Module):
def __init__(self, ni, nf):
self.convs = nn.Sequential(
ConvLayer(ni, nf),
ConvLayer(nf, nf, norm_type=NormType.BatchZero)
)
def forward(self, x):
return x + self.convs(x)
By passing NormType.BatchZero to the second convolutional layer, we initialize the $\gamma$s in the batchnorm equation to 0.
Although we could begin training with the ResBlock, how would x + F(x) work if x and F(x) are of different shapes?
Well, how could they become different shapes? When ni != nf or we use a stride that's not 1. Remember that x has the shape n_batch * n_channels * height * width. If we have ni != nf, then n_channels is different for x and F(x). Similarly, if stride != 1, then height and width would be different for x and F(x).
Instead of accepting these restrictions, we can resize x to become the same shape as F(x). First, we appply average pooling to change height and width, then apply a 1 $\times$ 1 convolution (a convolution layer with a kernel size of 1 $\times$ 1) with ni in-channels and nf out-channels to change n_channels.
Through changing our code, we have:
def _conv_block(ni, nf, stride):
return nn.Sequential(
ConvLayer(ni, nf, stride=stride),
ConvLayer(nf, nf, act_cls=None, norm_type=NormType.BatchZero)
)
class ResBlock(Module):
def __init__(self, ni, nf, stride=1):
self.convs = _conv_block(ni, nf, stride)
# noop is `lamda x: x`, short for "no operation"
self.idconv = noop if ni == nf else ConvLayer(ni, nf, 1, act_cls=None)
self.pool = noop if stride == 1 else nn.AvgPool2d(stride, ceil_mode=True)
def forward(self, x):
# we can apply ReLU for both x and F(x) since we specified
# no activation functions for the last layer of conv and idconvs
return F.relu(self.idconv(self.pool(x)) + self.convs(x))
In our new ResBlock, one pass will lead to H(G(x)) + F(x) where F is two convolutional layers and G is a pooling layer followed by H, a convolutional layer. We have a pooling layer to make the height and width of x the same as F(x) and the convolutional layer to make G(x) have the same out-channels as F(x). Then, H(G(x)) and F(x) will have the same shape all the time, allowing them to be added. Overall, a resnet block is 2 layers deep.
def block(ni, nf):
return ResBlock(ni, nf, stride=2)
So, let's try retraining with the new model:
learn = get_learner(get_model())
learn.fit_one_cycle(5, 3e-3)
We didn't get much of an accuracy boost, but that's because we still have the same number of layers. Let's double the layers:
def block(ni, nf):
return nn.Sequential(ResBlock(ni, nf, stride=2), ResBlock(nf, nf))
learn = get_learner(get_model())
learn.fit_one_cycle(5, 3e-3)
The first step to go from a resblock to a resnet is to improve the stem of the model.
The first few layers of the model are called its stem. Through practice, some researchers found improvements by beginning the model with a few convolutional layers followed by a max pooling layer. A max pooling layer, unlike average pooling, takes the maximum instead of the average.
The new stem, which we prepend the the model looks like this:
def _resnet_stem(*sizes):
return [
ConvLayer(sizes[i], sizes[i + 1], 3, stride=2 if i == 0 else 1)
for i in range(len(sizes) - 1)
] + [nn.MaxPool2d(kernel_size=3, stride=2, padding=1)]
Keeping the model simple in the beginning helps with training because with CNNs, the vast majority of computations, not parameters, occur in the beginning where images have large dimensions.
_resnet_stem(3, 32, 32, 64)
These same researchers found additional "tricks" to substantially improve the model: using four groups of resnet blocks with channels of 64, 128, 256, and 512. Each group starts with a stride of 2 except for the first one since it's after the max pooling layer from the stem.
Below is the resnet:
class ResNet(nn.Sequential):
def __init__(self, n_out, layers, expansion=1):
stem = _resnet_stem(3, 32, 32, 64)
self.channels = [64, 64, 128, 256, 512]
for i in range(1, 5): self.channels[i] *= expansion
blocks = [self._make_layer(*o) for o in enumerate(layers)]
super().__init__(*stem, *blocks,
nn.AdaptiveAvgPool2d(1), Flatten(),
nn.Linear(self.channels[-1], n_out))
def _make_layer(self, idx, n_layers):
stride = 1 if idx == 0 else 2
ni, nf = self.channels[idx:idx + 2]
return nn.Sequential(*[
ResBlock(ni if i == 0 else nf, nf, stride if i == 0 else 1)
for i in range(n_layers)
])
The "total" number of layers in a resnet is double sum of the layers passed in as layers in instantiating ResNet plus 2 from stem and nn.Linear. We consider stem as one layer because of the max pooling layer at the end.
So, a resnet-18 is:
rn18 = ResNet(dls.c, [2, 2, 2, 2])
rn18
Where it has 18 layers since we pass in [2, 2, 2, 2] for layers, which sums of 8 and double that is 16 (we double since each ResBlock is 2 layers deep). Then, we add 2 from stem and nn.Linear to get 18 "total" layers.
By increasing the number of layers to 18, we see a significant increase in our model's accuracy:
learn = get_learner(rn18)
learn.fit_one_cycle(5, 3e-3)
As you increase the number of layers in a resnet, the number of parameters increases substantially. Thus, to avoid running out of GPU memory, we can apply bottlenecking, which alters the convolutional layer in ResBlock for F in x + F(x) as follows:
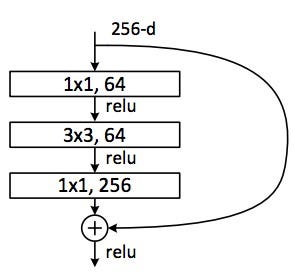
Previously, we stacked two convolutions with a kernel size of 3. However, a bottleneck layer has a convolution with a kernel size of 1, which decreases the channels by a factor of 4, then a convolution with a kernel size of 3 that maintains the same number of channels, and then a convolution with a kernel size of 1 that increases the number of channels by a factor of 4 to return the original dimension. It's coined bottleneck because we start with, in this case, a 256-channel image that's "bottlenecked" by the first convolution into 64 channels, and then enlarged to 256 channels by the last convolution.
Although we'll have another layer, it performs faster than the two convolutions with a kernel size of 3 because convolutions with a kernel size of 1 are much faster.
Through bottleneck layers, we can have more channels in more-or-less the same amount of time. Additionally, we'll have fewer parameters since we replace a 3 $\times$ 3 kernel layer with two 1 $\times$ 1 kernel layers, although one has 4 more out-channels. Overall, we have a difference of 4$:$9.
In code, the bottleneck layer looks like this:
def _conv_block(ni, nf, stride):
return nn.Sequential(
ConvLayer(ni, nf // 4, stride=1),
ConvLayer(nf // 4, nf // 4, stride=stride),
ConvLayer(nf // 4, nf, stride=1, act_cls=None, norm_type=NormType.BatchZero)
)
Then, when we make our resnet model, we'll have to pass in 4 for our expansion to account for the decreasing factor of 4 in our bottleneck layer.
rn50 = ResNet(dls.c, [3, 4, 6, 3], 4)
learn = get_learner(rn50)
learn.fit_one_cycle(20, 3e-3)
In the previous blog, we achieved a 99.2% accuracy with just the CNN. Let's try training a resnet-50 with the MNIST data set and see what we can get:
def get_dls(url, bs=512):
path = untar_data(url)
return DataBlock(
blocks=(ImageBlock(cls=PILImageBW), CategoryBlock),
get_items=get_image_files,
splitter=GrandparentSplitter('training', 'testing'),
get_y=parent_label,
batch_tfms=Normalize()
).dataloaders(path, bs=bs)
dls = get_dls(URLs.MNIST)
dls.show_batch(max_n=4)
We have to change the first input into _resnet_stem to 1 from 3 since the MNIST data set is a greyscale image.
class ResNet(nn.Sequential):
def __init__(self, n_out, layers, expansion=1):
stem = _resnet_stem(1, 32, 32, 64)
self.channels = [64, 64, 128, 256, 512]
for i in range(1, 5): self.channels[i] *= expansion
blocks = [self._make_layer(*o) for o in enumerate(layers)]
super().__init__(*stem, *blocks,
nn.AdaptiveAvgPool2d(1), Flatten(),
nn.Linear(self.channels[-1], n_out))
def _make_layer(self, idx, n_layers):
stride = 1 if idx == 0 else 2
ni, nf = self.channels[idx:idx + 2]
return nn.Sequential(*[
ResBlock(ni if i == 0 else nf, nf, stride if i == 0 else 1)
for i in range(n_layers)
])
rn50 = ResNet(dls.c, [3, 4, 6, 3], 4)
learn = get_learner(rn50)
lr = learn.lr_find().valley
learn.fit_one_cycle(20, lr)
After training the model by 20 epochs, we can confidently say that it's not always the best idea to start with a more complex architecture that takes much longer to train and gives a worse accuracy.
In addition, I mentioned before that resnets aren't the best for OCR problems like digit recognition since we're slicing the image and deciding, on average, what the digit is.
In this scenario, a regular CNN would be a better choice than a resnet.
In this blog, we covered residual networks, which allow us to train CNNs with more layers by having the model learn indirectly through residuals. It's as if before, we were just training the weights of the activations, when in reality, we also needed bias to have the models learn efficiently. To visualize, imagine the following:
Before, we had
weights * x + biasas our activations, where x is our input. But, that just gives us activations. Through residual networks, we have
(weights * x + bias) + residualswhich adds on another parameter that we can train. Through exploring, we found that we'd need some way to make (weights * x + bias) have the same shape as residuals to allow them to be added. Thus, we formed
reshape * (weights * x + bias) + residualsTherefore, a residual network fixes a CNN to be more like how we train neural networks since the above can be simplified to:
weights * x + biasThen, to use this new kind of layer, we had to use fully convolutional networks that allow us to have input of any shape. Finally, we looked at a bag of tricks like stems, groups, and bottleneck layers that allow us to train RNNs more efficiently and have many more layers.
At this point, we've covered all the main architectures for training great models with computer vision (CNN and resnet), natural language processing (AWD-LSTM), tabular data (random forests and neural networks), and collaborative filtering (probabilitic matrix factorization and neural networks).
From now on, we'll be looking at the foundations of deep learning and fastai through modifying the mentioned architectures, building better optimization functions than the standard SGD, exactly what PyTorch is doing for us, how to visualize what the model is learning, and a deeper look into what fastai is doing for us through its Learner class.