What are Convolutional Neural Networks?
And here we thought we'd be done with linear algebra...
Before we look at convolutional neural networks, we should look at what a convolution is.
Convolutions are a kind of feature engineering, which is transforming data to make it easier to model. With tabular data, we used add_datepart to split the date column into many metacolumns. The metacolumns (and the initial date column) are what we call features.
So, what kind of features can we make with images? With images, a feature is something that is visually distinctive. If we can't see it, it's unlikely the computer can see it. But, what if it's there and it's just difficult to see it at first glance? That's where we use convolutions.
A convolution is an operation that applies a kernel across channels of an image.
An image can be thought of as a three dimensional matrix: channel $\times$ height $\times$ width where channel can be indexed for the brightness of a single colour. In RGB images, we have three channels: red, green, and blue. In greyscale images, we have one channel: white.
A kernel is a square matrix that's applied to each channel of the image. For instance, the following 3 $\times$ 3 kernel is used to amplify horizontal edges, particularly the top edges:
top_edge = tensor([-1, -1, -1],
[ 0, 0, 0],
[ 1, 1, 1]).float()
top_edge
When we apply a kernel across an image, we multiply a (valid) subtensor of the same shape as our kernel and take the sum as illustrated by this gif:
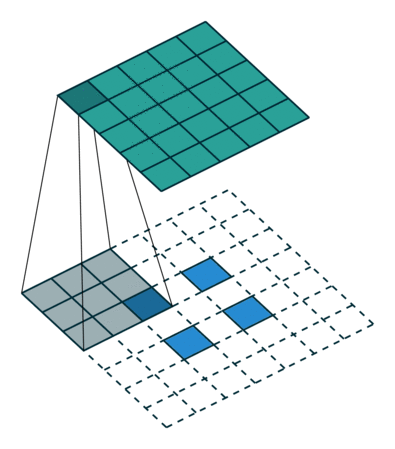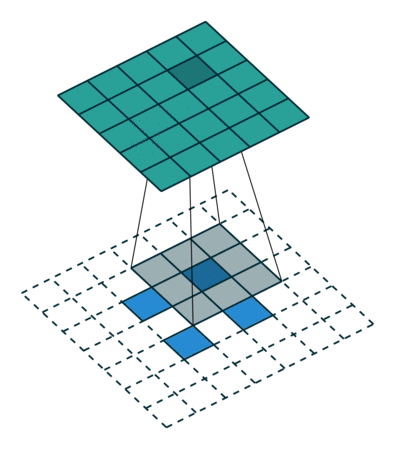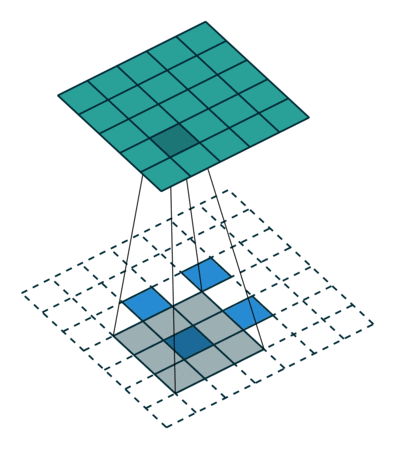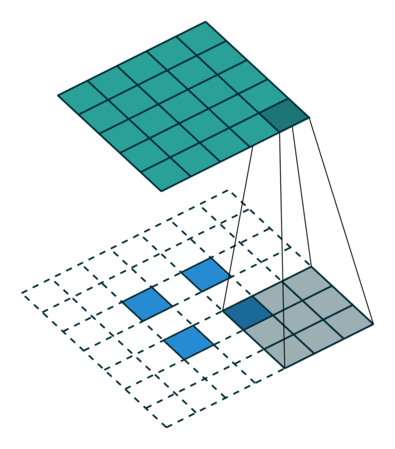
The subtensor is valid when every item in the kernel can be mapped to a unique item in the subtensor. So, we can't have a subtensor where the center is along an edge.
To show the kernel in action, we can define a function that applies what we described above:
def apply_kernel(img, row, col, kernel):
# Through our indexing, you can see how having the center (row, col)
# along the edge would cause errors with indexing
return (img[row - 1:row + 2, col - 1:col + 2] * kernel).sum()
And we'll get an image:
path = untar_data(URLs.MNIST_SAMPLE)
Path.BASE_PATH = path
img = tensor(Image.open(path/'train'/'3'/'52269.png')).float()/255
show_image(img);
Then, we can use list comprehension to show the convoluted image:
r = range(1, 27)
img_ = tensor([[apply_kernel(img, i, j, top_edge) for j in r] for i in r])
show_image(img_);
To simplify it for future images, we can put the above convolution process into a function:
def apply_kernel_img(img, kernel):
w = kernel.shape[0] // 2
r = range(w, img.shape[0] - w)
return tensor([[apply_kernel(img, i, j, kernel) for j in r] for i in r])
Next, we can create a few more kernels:
bot_edge = tensor([ 1, 1, 1],
[ 0, 0, 0],
[-1, -1, -1]).float()
lef_edge = tensor([-1, 1, 0],
[-1, 1, 0],
[-1, 1, 0]).float()
And try them out:
show_image(apply_kernel_img(img, bot_edge), title='Bottom'), show_image(apply_kernel_img(img, lef_edge), title='Left');
You can see how in our apply_kernel_img function that we create our range with bounds. If our kernel is 3 $\times$ 3, then our w becomes 1 and we need our center to be 1 pixel apart from the edge at all times. In general, if a kernel is k $\times$ k (with k being odd since an even kernel is almost never seen in practice and would require different padding on each side), then our center needs to stay k // 2 apart from the edge.
But, what if we could pad the edges? Then, we would be able to have our original image size returned when we apply a convolution; like this:

So with padding, we get to retain all the information from the image.
However, we don't always want the original image size returned. Therefore, we have the idea of strides, where a stride-n convolution applies the convolution every n pixels.

Overall, each dimension of the convoluted image will be of size (n + 2 * pad - k) // stride + 1, where n is the original size for the image, pad is the padding, k is the kernel size and stride is the stride. So, for the above example, we have n = 5, pad = 3 // 2 = 1, k = 3, and stride = 2 so our resulting image will have dimensions of (5 + 2 * 1 - 3) // 2 + 1 = 3 thus 3 $\times$ 3.
Now that we've learned about strides, let's implement it in our previous function:
def apply_kernel_img_w_stride(img, kernel, stride=2):
w = kernel.shape[0] // 2
r = range(w, img.shape[0] - w, stride)
return tensor([[apply_kernel(img, i, j, kernel) for j in r] for i in r])
Through striding, we get:
imgs = apply_kernel_img_w_stride(img, bot_edge), apply_kernel_img_w_stride(img, lef_edge)
show_image(imgs[0], title='Bottom'), show_image(imgs[1], title='Left');
Where the shape of our tensors are halved:
imgs[0].shape
We've looked at convolutions, padding, and strides. How can we put them inside a neural network to get a convolution neural network (abbreviated to CNN)?
With LSTM RNNs, we made our model learn the importance of what to remember and what to forget. We can do the same with CNNs; actually, we can do the same with basically any neural network since it's based off of SGD: instead of defining our own kernels, we make our model learn its own kernels.
A neural network that uses convolutions instead of, or in addition to, linear layers is what we call a CNN.
Say we have a simple neural network like:
simple_nn = nn.Sequential(
nn.Linear(28 * 28, 30),
nn.ReLU(),
nn.Linear(30, 1)
)
simple_nn
We can turn it into a simple CNN by replacing the nn.Linear layers with nn.Conv2d layers which are convolutional layers (in 2-dimension):
simple_cnn = nn.Sequential(
nn.Conv2d(1, 30, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(30, 1, kernel_size=3, padding=1)
)
simple_cnn
With CNNs, we don't need to specify the size of the input image like in simple_nn. A linear layer needs a weight in the weight matrix for each pixel, but with a convolutional layer, we only need to define the kernel's size and the kernel is applied to each pixel automatically. The weights of the kernel only depend on the number of input and output channels and the kernel size.
So, why do we use strides? Well, the output of our simple_cnn has the following shape:
db = DataBlock((ImageBlock(cls=PILImageBW), CategoryBlock),
get_items=get_image_files, splitter=GrandparentSplitter(),
get_y=parent_label)
dls = db.dataloaders(path)
xb, yb = first(dls.valid)
xb, yb = to_cpu(xb), to_cpu(yb)
simple_cnn(xb).shape
Instead of getting two activations that we can use for classification between 3s and 7s, we get 28 $\times$ 28 activations. One way we can narrow down to two activations is to use a stride of 2, where we half the dimensions of each output image with each layer.
By default, nn.Conv2d has a stride of (1, 1), which is 1 horizontally and 1 vertically. Since we don't want to define kernel_size and padding each time, we can refactor a layer like so:
def conv(in_channels, out_channels, kernel_size=3, nonlinearity=True):
layer = nn.Conv2d(in_channels, out_channels,
kernel_size=kernel_size, padding=kernel_size//2,
stride=2)
if nonlinearity:
layer = nn.Sequential(layer, nn.ReLU())
return layer
Then, we can make a new model where we half our way to 2 activations for a 1 $\times$ 1 image:
simple_cnn = nn.Sequential(
conv(1, 4), # 14x14
conv(4, 8), # 7x7
conv(8, 16), # 4x4
conv(16, 32), # 2x2
conv(32, 2, nonlinearity=False), # 1x1
Flatten()
)
With this new model, our resulting shape is:
simple_cnn(xb).shape
Next, we'll make a Learner with our model:
learn = Learner(dls, simple_cnn, loss_func=F.cross_entropy, metrics=accuracy)
Then, with the summary method, we can see how the shape of the output changes at each layer:
learn.summary()
Our last conv layer produces a tensor of shape 64 x 2 x 1 x 1, but we only want 64 x 2, so we use Flatten to remove the extra 1 x 1 axes.
Because it's a deeper network than simple_nn, we'll have to train it with a lower learning rate with more epochs:
learn.fit_one_cycle(4, 1e-2)
When we use a stride of 2, we decrease the number of activations by a factor of 4 at each layer because the height and the width of the output image are being halved.
The number of trainable weights for a given layer is out_channels * in_channels * kernel_height * kernel_width. PyTorch has the axes of the tensor in the order of in_channels, out_channels, kernel_height, kernel_width:
simple_cnn[0][0].weight.shape
So, we have 36 weights for the first layer. The number of trainable parameters, which is given in the summary is weights + biases. For each layer, the number of biases is equal to the number of out_channels. Since there's 4 out-channels for the first layer, the total trainable parameters is 40.
If we look at the multiplications the model is doing, at each layer the model is doing image_height * image_width * weights multiplications. Since the output image decreases by a factor of 4 after each layer, the number of multiplications also decreases by a factor of 4 for the next layer if we held the number of weights constant. To keep the number of multiplications the same or larger, we need to increase the number of channels (i.e. features) at each level.
Starting with a higher out-channel and then doubling it after each layer ends up working out since the in-channel of the next layer is double that of the current and the out-channel of the next layer is double that of the current. So, we get a total increase by a factor of 4.
Why do we even need to multiply the same or even more for later layers? Well, it wouldn't make sense for the later layers, which are meant to be learning semantically rich features, to be doing fewer computations than the earlier layers.
Don't believe me? Let's try it with our current data set and see how our accuracy differs:
bad_cnn = nn.Sequential(
conv(1, 4),
conv(4, 4),
conv(4, 4),
conv(4, 4),
conv(4, 2, nonlinearity=False),
Flatten()
)
learn = Learner(dls, bad_cnn, loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(4, 1e-2)
Unsurprisingly, the accuracy is a bit worse. However, it's also not worse by much. Does that mean our previous hypothesis of "later layers should have more computations than earlier layers" is false? Not really. Our current data set is just comparing two different categories: 3s and 7s. It's when we get to more complex image categories (or more categories) that we'll see a larger drop in accuracy.
Before we get to the full MNIST data set, let's look at how we can deal with images other than greyscale images.
Well, a double rainbow is a phenomenon of optics that displays a spectrum of light due to the sun shining on droplets of moisture in the atmosphere. Does that explain it?
With each convolutional layer, we have in_channels and out_channels; that is, for each out_channels, there's in_channels kernels that are each of size kernel_height $\times$ kernel_width. These kernels are the weights that we train and as mentioned before, have weights that total to out_channels * in_channels * kernel_height * kernel_width. The total trainable parameters is equal to the total weights and the total biases. We don't have separate biases for each weight. Instead, we have a bias for each set of in_channels kernels, and, how many are there? There's out_channels sets.
But what exactly are in-channels and out-channels? Let's look at the first layer. For a greyscale image, we had an in-channel of 1, whose "feature" is a 2 dimensional tensor that contains the brightness for each pixel. With an out-channel of size $n$, we want out_channels ($n$) sets of in_channels kernels, each of size kernel_height $\times$ kernel_width, and each with a bias, that will somehow (trained through SGD) create $n$ different images that each depict (hopefully) a unique feature (i.e. channel) that can be helpful in classification; that's what I mentioned at the beginning of this blog:convolutions are a kind of feature engineering, which is transforming data to make it easier to model (classify).
How does out_channels in_channels kernels work together? For each set (which is a set of in_channels kernels), each kernel is applied to its appropriate channel, which results in in_channels images. These images can be stacked and each stacked pixel are summed to result in a single tensor of shape new_image_height $\times$ new_image_width. Overall, we'll have out_channels of these "images" (technically, they're features; technically-technically, they're channels) that we feed as input for the next layer, or use for classification.
With the way I'm using the terms images, features, and channels, it can be a little confusing as to what they mean.
One of the channels of an image would be the 2 dimensional tensor that's being used as the initial input, or a part of the output of each layer (the last 2 axes).
Features and channels are essentially the same: they're the second axis of the output, which is how many activations there are for each output image pixel.
In general, they're actually "features" that you can take from an image like edges, which we showed in the beginning through actual code, gradients, colour, and other kinds of things.
The only difference between features and channels is that features are only used to describe the output of the layer (what we actually get after we apply the kernels), while channels can refer to both the input and the output (hence, why we have in_channels and out_channels instead of in_features).
So, what's this about a double rainbow? Well, what do rainbows have? Colour! How can we incorporate coloured images into a CNN? It's actually really simple: instead of starting with an in_channels of 1 (currently used for the brightness of each pixel), we start with the appropriate number required to describe the image. An RGB image has an in_channels of 3: one for red, green, and blue. An RGBA image (Red-Green-Blue-Alpha) has an in_channels of 4.
What's even crazier is that it doesn't matter what colour scheme you use to describe your image when training: the results aren't that different. BUT, this rule only applies if no information is lost when you change the colour scheme. For example, going from a greyscale to a coloured image is fine since the image is still greyscale. But, going from a coloured image to greyscale is going to give different results since you're losing all the information that comes with colour.
In becoming a master of digits, one must be able to classify every digit in a handwritten number. You may not have noticed it, but we're already one step ahead by using fit_one_cycle on our learner.
Fastai actually has a fit function that you can use to train your model instead of fit_one_cycle. fit_one_cycle doesn't mean fit for one cycle (i.e. epoch). It actually implements 1cycle.
The foundation of 1cycle training is that our randomized initial weights aren't suited for our task so it's a bad idea to start with a high learning rate: we may diverge instantly (get far away from a low loss) and skip over a minimum loss near the end of training.
So, what if we had a "cycle" using "1" learning rate, where we start with a learning rate lower than the given learning rate, gradually make our way to the maximum learning rate, and then go back down to a lower learning rate? By doing so, we get two benefits:
- we can train faster since we take bigger steps at the optimization stage; and
- we overfit less since we skip sharp minimums, which may not be "minimums" at the slightest change.
Why do we get these benefits? We start with a lower learning rate so our loss won't explode to crazy places; eventually, we end up in a pretty smooth area. Then, we increase the learning rate, gradually, to the maximum learning rate. Since we're already in a smooth region (thus lower gradients), we step by a larger amount, but we aren't stepping by a crazy amount. Then, we eventually settle into a very nice smooth region and we begin lowering our learning rate to get the very nice minimum loss.
Instead of slowly inching towards a good minimum through a low learning rate, we inch a little in the beginning, zoom to a good place, and then inch again to a nice minimum.
So, let's try training our simple_cnn model using fit and see how our accuracy changes:
learn = Learner(dls, simple_cnn, loss_func=F.cross_entropy, metrics=accuracy)
learn.fit(4, 1e-2)
It doesn't decrease by much. Is 1cycle unnecessary? Let's try downloading the full MNIST data set and training it with fit.
path = untar_data(URLs.MNIST)
Unlike the sample MNIST data set, which contains just 3s and 7s, we get all the digits in this data set. But, it's also stored differently:
!ls {path}
We have our data separated into two folders: testing and training. In each folder, we have subfolders that contain images for each digit:
!ls {path}/training
So, we'll have to tell our DataBlock to make our DataLoaders differently:
def get_dls(bs=64):
return DataBlock(
blocks=(ImageBlock(cls=PILImageBW), CategoryBlock),
get_items=get_image_files,
splitter=GrandparentSplitter('training', 'testing'),
# GrandparentSplitter defaults to 'train' and 'test'
# so we'll have to tell it to look at different folders
get_y=parent_label,
batch_tfms=Normalize() # we also normalize the batches so that our input
# batch is within a similar range of numbers
).dataloaders(path, bs=bs)
dls = get_dls()
To make sure we got our images correctly, we can look at a batch:
dls.show_batch(max_n=9, figsize=(4, 4))
Now that we have our input data prepared, we'll have to make some adjustments to our simple_cnn since we're now dealing with 10 possible outputs instead of 2.
def simple_cnn():
return sequential(
conv(1, 8, kernel_size=5),
conv(8, 16),
conv(16, 32),
conv(32, 64),
conv(64, 10, nonlinearity=False),
Flatten()
)
This time, we start with more out-channels (because there'll be more features to distinguish between all digits compared to just 3s and 7s) and end with more out-channels (10 out-channels since we have 10 digits to classify).
We also change the initial kernel size since we wouldn't expect the model to learn 8 different features by looking at 9 pixels at a time. Instead, it'd be better for the model to learn 8 unique features by looking at 25 pixels at a time (through a kernel size of 5 $\times$ 5).
Now, let's train this model:
# We default to a higher learning rate so that we can
# keep training time short while making changes
def fit(epochs=1, lr=6e-2):
learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
metrics=accuracy, cbs=ActivationStats(with_hist=True))
learn.fit(epochs, lr)
return learn
learn = fit()
See? We can't even get a 10% accuracy with just fit when we have a more complex data set.
To see why we're having such a bad accuracy, let's look at the activations (which we can since we added the ActivationStats CallBack that records the mean, standard deviation, and a histogram of every activation from every trainable layer):
learn.activation_stats.plot_layer_stats(0)
The x-axis of these graphs are the batches and the y-axis is given by the graph's name.
Ideally, we want our activations to have a smooth mean and standard deviation because that means our training is stable (i.e., isn't leading to sudden changes).
Currently, our first layer is training smoothly, but is getting increasing amounts of activations near zero.
Let's see what the final point means for our penultimate (second-last) layer:
learn.activation_stats.plot_layer_stats(-2)
The mean is getting to a constant (a bit too smooth) and our standard deviation is getting very close to 0. Why might this be the case? Almost all our activations are 0 by the time we get to the later layers. Just what is our model learning?
We don't want many activations near 0 since that means our model is disregarding information. We also don't want an increasing trend of "zero" activations because it snowballs for the later layers since multiplying by zero gives zero.
So, let's try improving our training stability by using 1cycle:
def fit(epochs=1, lr=6e-2):
learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
metrics=accuracy, cbs=ActivationStats(with_hist=True))
learn.fit_one_cycle(epochs, lr)
return learn
learn = fit()
We can inspect what 1cycle's doing through the Recorder callback. It starting with a lower learning rate, gradually increases to the given maximum (6e-2), then goes back to the lower one. We can see the changes across the batches through the left graph:
learn.recorder.plot_sched()
The right graph shows the change in momentum. Momentum, like the name indicates, keeps the optimizer stepping in the same direction as it did in the previous steps. Momentum is also changed according to 1cycle, although in the opposite direction (high-low-high).
Overall, we see a great improvement in our accuracy. But, is our activations more stable?
learn.activation_stats.plot_layer_stats(-2)
Not really... we see a few spikes here and there, but it eventually stabilizes. However, we also see that a lot of our activations get close to 0. And, we start with an unusually high number of "zero" activations. Why might this be the case?
Before we look into why and how we can fix it, let's look at this problem from a different perspective. Fastai also provides a colorful dimension graph, which plots histograms of the activations from each batch along the x-axis, where colormaps are used to simulate the height, hence viewing the height through the "colorful dimension".
The activations are log'd before they're recorded in the histograms, which is why the means displayed above are negative: the closer to 0, the closer to negative infinity in terms of log:
So, our colorful dimension graph for our penultimate layer is:
You should imagine the graph above to be the upper portion of what would be a mirrored graph along the x-axis.
If you're having trouble linking the colormap to height, this graph in 3-dimensions looks like this:
def color_dim3d(idx=-2, elev=90, azim=-90, cmap='inferno'):
res = learn.activation_stats.hist(idx)
res.shape
fig = plt.figure(figsize=(20, 15), constrained_layout=True)
ax = plt.gca(projection='3d')
x, y = res.shape
X, Y = np.mgrid[0:x, 0:y]
# ax.set_xlim3d(0, y)
# ax.set_ylim3d(0, x)
# ax.set_zlim3d(res.min().item(), res.max().item())
x_scale=1
y_scale=0.5
z_scale=0.1
scale=np.diag([x_scale, y_scale, z_scale, 1.0])
scale=scale*(1.0/scale.max())
scale[3,3]=1.0
def short_proj():
return np.dot(Axes3D.get_proj(ax), scale)
ax.get_proj=short_proj
ax.plot_surface(Y, X, res, cmap=cmap, rcount=50, ccount=150)
ax.view_init(elev, azim)
ax.grid(False)
ax.axis('off')
plt.savefig('a.png', bbox_inches='tight')
The colorful dimension graph shows that we have a case of "bad training" where over the first few batches the number of nonzero activations exponentially increases, but then it crashes and over the next course of batches, the model basically learns again from the beginning, but with less "zero" activations. This cycle repeats until it eventually reaches a decent spread of activations.
So, we've looked at the statistics based on the activations. There's decent stability near the end of the training, but why can't we have that stability in the beginning?
Maybe we have a few batches that're much different compared to the other one. Those few odd batches may be causing a set of much different activations.
Then, what's a way we can reduce the odds of a batch being more different? If we look at probability, we can make the odds smaller by increasing the denominator. Therefore, we increase the batch size:
dls = get_dls(512)
With a larger batch size, we get to calculate our activations with more data, so our gradients will be more accurate. However, we'll have fewer batches per epoch, meaning we'll have fewer steps in the loss per epoch.
learn = fit()
We see an improvement in accuracy. Let's look at the activations of our penultimate layer:
learn.activation_stats.plot_layer_stats(-2)
Althrough the curves do look smoother, and we have less activations near zero, we still start with a very high number of zero activations, which leads to the same problem that's shown in the colorful dimension graph:
learn.activation_stats.color_dim(-2)
Is the stability of our model's training doomed?
Well, we're looking at the activations, remember? What can we do to fix much different activations that can also smoothen the mean and standard deviation? Normalization.
Normalization can even eliminate the higher number of near zero activations in the beginning since they'll be spread out along a normal distribution.
So, let's talk about batch normalization; this process isn't applied to batches given by DataLoaders (which is already handled by the Normalize we passed to batch_tfms in our DataBlocks), but is applied to a batch of activations given by a layer. Therefore, we add a layer that applies batch normalization, which we call batchnorm, after each "layer" (a linear/convolutional layer and an optional nonlinearity).
However, life isn't so simple and the values returned through normalization are small. Sometimes, the network needs larger activations to make good predictions; so, if a normalized activation is $y$, then the batchnorm layer actually returns $\gamma y + \beta$, where $\gamma$ and $\beta$ are trainable parameters that are changed at every batch during the optimization step.
Consequently, batchnorm allows us to have any mean or variance in our activations, independent from the activations of the previous layers. Additionally, a model containing batchnorm tends to generalize better because of the additional parameters $\gamma$ and $\beta$ that work to account for varying means and variances amongst activations from different batches of input.
Finally, we normalize the activations differently depending on training and during inference. At training, we use the mean and standard deviation of the batch; but, during inference, we normalize by using the mean of the statistics (mean and standard deviation) of the batches that we had during training.
def conv(in_channels, out_channels, kernel_size=3, nonlinearity=True):
layers = [nn.Conv2d(in_channels, out_channels, kernel_size,
stride=2, padding=kernel_size//2)]
if nonlinearity:
layers.append(nn.ReLU())
layers.append(nn.BatchNorm2d(out_channels))
return nn.Sequential(*layers)
# the * unpacks the list into a sequence of elements
learn = fit()
learn.activation_stats.plot_layer_stats(-2)
Now, although our mean is still unsteady in the beginning, our standard deviation is much more stable and we have much less activations near zero in the beginning.
All these changes can also be seen through the colorful dimension graph:
learn.activation_stats.color_dim(-2)
With the above graph, we start with mostly near zero activations, which then become more distributed and stay distributed through a stable standard deviation.
Using what we've covered thus far, let's train a model using more epochs and a higher learning rate (which batchnorm enables):
learn = fit(5, 0.1)
Our colorful dimension graph indicates "good training" through its shape:
learn.activation_stats.color_dim(-2)
In a previous blog, we trained a CNN-based architecture, resnet18, on the MNIST data set using cnn_learner and fit_one_cycle to get an accuracy of 98.3% after fine-tuning for 1 epoch at a 0.1 learning rate.
In this blog, we've covered what convolutions are and how they're used to create convolutional layers in a convolutional neural network. We've trained a model using a simple CNN on a sample MNIST data set to compare 3s and 7s. However, we've found that task to be too simple. Thus, we moved onto the full MNIST data set. Little did we know, our simple CNN from before wouldn't even be able to get a 10% accuracy; it's worse than a chimp.
We began with too high of a learning rate. But, if we kept lowering it, our training would take far too long. Luckily, 1cycle allows us to have that learning rate as our maximum and we'll be able to train quickly, while taking advantage of lower learning rates. Nonetheless, we still had some instability in our training. As we saw with the colorful dimension graphs, our model had too many initial zero activations and it caused our model to explode and collapse, retraining basically from scratch after a few batches. Thankfully, we've learned about batch normalization and that gave us the stability we needed to train our model and end up with an accuracy of 99.2%.
Not only did we beat the result on our previous blog, we even learned how everything works to get that score.
In the next blog, we'll be looking at residual networks (i.e. resnet) and how we can use that to get an even better score.