What are Recurrent Neural Networks?
Wait it's all a fancy loop?
In a previous blog, we used a pretrained model that used the AWD-LSTM architecture. This architecture is built off a recurrent neural network. "Recurrent", according to Cambridge Dictionary means "happening again many times". And it just so happens that a recurrent neural network is a neural network with layers that happen again (repeat) many times.
To go over RNNs in this blog, we'll be using the human numbers data set that contains the first 10,000 numbers written out in English.
We'll download the data set from fastai's URLs class:
from fastai.text.all import *
path = untar_data(URLs.HUMAN_NUMBERS)
Then, we'll see how the data set is laid out:
path.ls()
There's two text files that contain the numbers. Since we're creating a language model, we'll concatenate them:
lines = L()
with open(path/'train.txt') as f:
lines += L(f.readlines())
with open(path/'valid.txt') as f:
lines += L(f.readlines())
lines
Then, we can join the lines together, separated by dots so that we can tokenize them:
text = ' . '.join([i.strip() for i in lines])
text[:100]
We'll then tokenize them by splitting them according to spaces:
tokens = text.split(' ')
tokens[:10]
We first joined them with a period instead of spaces because the spaces between the words are significant. We want to separate numbers, not words, as in, we want this:
text[text.rindex('.'):]
Not this:
nine . thousand . nine . hundred . ninety . nineNext, we'll create our vocab by making a list of the unique tokens:
vocab = L(tokens).unique()
vocab
And then we'll numericalize the tokens. In this blog, we'll be keeping the notation of input_target like "input" to (_) "target", so t_i means token to index:
t_i = {t: i for i, t in enumerate(vocab)}
nums = L(t_i[t] for t in tokens)
nums[:10]
We want our model to predict the next word given the last 3 words in the sequence, so we can do that with just Python:
seqs_tok = L((tokens[i:i+3], tokens[i+3]) for i in range(0, len(tokens)-4, 3))
seqs_tok
And since it looks right with the tokens, we'll do the same with the numericalized tokens (and it should look like the above, but with numericalized tokens instead):
seqs = L((tensor(nums[i:i+3]), nums[i+3]) for i in range(0, len(nums)-4, 3))
seqs
Then, we'll make our DataLoaders:
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], bs=64, shuffle=False)
And check that we can make a batch:
dls.one_batch()
For a model that takes in 3 words as input and tries to predict the next word, we can:
- Calculate the embeddings for the first word,
- Pass the embeddings into a linear layer,
- Apply a nonlinearity (like ReLU or softmax),
- Calculate the embeddings for the second word,
- Add the embeddings to the activations from step 3,
- Pass the activations into the same linear layer in step 2,
- Apply a nonlinearity, and
- Repeat steps 4 to 7 with the third word.
By adding the next word's embeddings to the previous activations, every word is interpreted in the context of the preceding words. And, we use the same weight matrix (linear layer) since the way one word influences the activations from the previous words shouldn't change depending on the position of the word; so, we force the layer to learn all positions instead of limiting each layer to one position.
To turn this idea into code, we can make a model by inheriting from PyTorch's Module class:
class RNNish(Module):
"""
We have three different states:
- Input (the words)
- Hidden (activations)
- Output (the probabilities for the next word)
We then have three different layers:
- i_h: input to hidden
- The embedding matrix to turn our words into embeddings
- h_h: hidden to hidden
- Calculates the activations for the next word
- h_o: hidden to output
- Calculates the predictions for the next word
"""
def __init__(self, n_vocab, n_hidden):
self.i_h = nn.Embedding(n_vocab, n_hidden)
# If we want a more complex model,
# we would be altering this
# hidden to hidden layer into more layers
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden, n_vocab)
# This is what our steps would look like
def forward(self, x):
h = self.i_h(x[:,0])
h = F.relu(self.h_h(h))
h = h + self.i_h(x[:,1])
h = F.relu(self.h_h(h))
h = h + self.i_h(x[:,2])
h = F.relu(self.h_h(h))
return self.h_o(h)
If you took any intro to CS course, you might've had a point where you didn't learn while loops yet so you were copy pasting if statements and changing a couple numbers here and there. Well, we know loops so we turn our repetitive "calculate the next embeddings, add it to the hidden state, then calculate the next activations" into a loop.
A hidden state is the activations that're updated at each step of a recurrent neural network (which we can see below in the for loop):
class RNN(Module):
def __init__(self, n_vocab, n_hidden):
self.i_h = nn.Embedding(n_vocab, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden, n_vocab)
# This is how we can simplify to turn it
# into a recurrent (looped) neural network
def forward(self, x):
# We can set it to 0 because tensors have
# a thing called "broadcasting" that tries
# to expand the smaller shape tensor into
# the same shape as the other one
h = 0
for i in range(3):
h = h + self.i_h(x[:,i])
h = F.relu(self.h_h(h))
return self.h_o(h)
So, a recurrent neural network is a neural network that's defined using a loop, hence recurrent. An RNN that isn't using a loop like RNNish is the unrolled representation of an RNN.
When we train a model with these two architectures, we should have about the same accuracy:
learn = Learner(dls, RNNish(len(vocab), 64), loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)
learn = Learner(dls, RNN(len(vocab), 64), loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)
And, we get about 49% for each. To see if it's actually good, we can compare it to if we just predicted the most commonly occurring token each time instead:
n, counts = 0, torch.zeros(len(vocab))
for x, y in dls.valid:
n += y.shape[0]
for i in range_of(vocab):
counts[i] += (y == i).long().sum()
idx = torch.argmax(counts)
idx, vocab[idx.item()], counts[idx].item()/n
So, if we just predicted the most commonly occurring token, "thousand", each time, we would have an accuracy of 15%, so our basic language model with an accuracy of 49% is much better.
You might be wondering, why don't you just use h += ... instead of h = h + ...? I thought so too, but you get a RuntimeError by PyTorch because you're using a tensor or its part to compute the tensor or its part; in other words, PyTorch can't calculate the gradient when you use +=. You can read more on why here.
Currently, we're initializing the hidden state h to 0 each time in forward. This effectively makes the model forget what it's seen before. To fix this, we can initialize h in __init__ and create a reset function to reinitialize h to 0.
But, this creates another problem: as we apply another layer to h, we add another thing on which we have to calculate the derivative during backpropagation. So, we can use PyTorch's detach method on h, which removes the gradient history of h (technically, it makes h no longer require gradient).
Overall, we made our new RNN stateful since it remembers its activations between different samples in the batch (between different calls to forward):
class RNN2(Module):
def __init__(self, n_vocab, n_hidden):
self.i_h = nn.Embedding(n_vocab, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden, n_vocab)
self.h = 0
def forward(self, x):
for i in range(3):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
out = self.h_o(self.h)
self.h = self.h.detach()
return out
def reset(self):
self.h = 0
We can also have any sequence length we want since we'll have the same activations each time. The only difference is that we only calculate the gradients on sequence length tokens in the past instead of all of them. This approach is called truncated backpropagation through time (truncated BPTT).
BPTT is treating an RNN as one big model (which we did by initializing h to 0 in __init__), and calculating gradients on it the usual way. Truncated BPTT avoids running out of memory and time by "detaching" the history of computation steps in the hidden state every (or few) epochs (which we did by reinitializing h to 0 in reset).
To make our model work, we need it to see the data set in order, such that dset[0] is in the first line of the first batch, dset[1] is in the first line of the second batch, and so on. For the other lines, we can split the data set into chunks of size m = len(dset) // bs, so dset[i + j * m] is in the j+1-th line of the i+1-th batch). This is done automatically in LMDataLoader.
The following function does the reindexing:
def group_chunks(dset, bs):
m = len(dset) // bs
new_dset = L()
for i in range(m):
new_dset += L(dset[i + j * m] for j in range(bs))
return new_dset
Then, when we make our DataLoaders, we also need to drop the last batch since it might not be of size bs. We also need to avoid shuffling the data since that would ruin the purpose of our reindexing.
bs = 64
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(
group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)
Finally, we need to adjust the training loop so that we call reset. We can do this by adding ModelResetter as a Callback (cbs), which calls reset before each epoch and each validation phase. Since we reinitialize the hidden state, we start with a clean state before each batch so we can train for more epochs.
learn = Learner(dls, RNN2(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(10, 3e-3)
Remember how when we took the movie review data set, we made the independent variable and dependent variable the same token length, but the dependent variable was ahead by one token? By doing so, we get more signal that we can feed back to the model when we update the weights. Why predict the last word of the sequence when you can predict the next word for each word in the sequence, right?
So, we can adjust our seqs to be of sl length for both independent and dependent variables, with them offset by one token:
sl = 16
seqs_lm = L((tensor(nums[i:i+sl]), tensor(nums[i+1:i+1+sl]))
for i in range(0, len(nums)-1-sl, sl))
[L(vocab[j] for j in seq) for seq in seqs_lm[0]]
Then we can make our DataLoaders the same way as before:
bs = 64
cut = int(len(seqs_lm) * 0.8)
dls = DataLoaders.from_dsets(
group_chunks(seqs_lm[:cut], bs),
group_chunks(seqs_lm[cut:], bs),
bs=bs, drop_last=True, shuffle=False)
But, we need to change our model so that it predicts after every word and not after the last one:
class RNN3(Module):
def __init__(self, n_vocab, n_hidden):
self.i_h = nn.Embedding(n_vocab, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden, n_vocab)
self.h = 0
def forward(self, x):
outs = []
# We changed 3 to sl since we'll be
# predicting the next word sl times
for i in range(sl):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
outs.append(self.h_o(self.h))
self.h = self.h.detach()
return torch.stack(outs, dim=1)
def reset(self):
self.h = 0
And, we'll have to flatten the inputs and targets before using them in F.cross_entropy. The output of the model has a shape bs $\times$ sl $\times$ n_vocab since we stacked the output onto one dimension (through dim=1). Our targets have shape bs $\times$ sl. So, we can reshape them using torch.view.
def loss_func(input, target):
# .view(-1, len(vocab)) means make len(vocab)
# columns with as many rows as needed (-1)
#
# .view(-1) means flatten the entire tensor
# into one row that's as long as it needs to be
return F.cross_entropy(input.view(-1, len(vocab)), target.view(-1))
Finally, we can train our model. We'll have to use an even larger number of epochs than last time because we have a more complex model:
learn = Learner(dls, RNN3(len(vocab), 64), loss_func=loss_func,
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
We got a better accuracy, but we have an effectively very deep network. So, we can end up with very small or very large gradients that can lead to very different results when we run train the model:
learn = Learner(dls, RNN3(len(vocab), 64), loss_func=loss_func,
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
By training a new model, we got a decrease of nearly 10% in accuracy. One way to fix this would be to try a deeper model: one with more than one linear layer between the hidden state and the output activations.
A multilayer RNN is more like a multiRNN model: we pass the activations from one RNN as inputs to another RNN.
This time, instead of creating a for loop, we can use PyTorch's nn.RNN class, which implements it for us while also letting us choose how many layers we want:
class RNN4(Module):
def __init__(self, n_vocab, n_hidden, n_layers):
self.i_h = nn.Embedding(n_vocab, n_hidden)
# Our inputs are in order of (bs, sl, n_vocab) so we have to
# tell PyTorch we want bs first instead of sl first
self.rnn = nn.RNN(n_hidden, n_hidden, n_layers, batch_first=True)
self.h_o = nn.Linear(n_hidden, n_vocab)
self.h = torch.zeros(n_layers, bs, n_hidden)
def forward(self, x):
acts, h = self.rnn(self.i_h(x), self.h)
self.h = h.detach()
return self.h_o(acts)
def reset(self):
self.h = self.h.zero_()
But, when we train our model, we get a worse accuracy than our previous single-layer RNN:
learn = Learner(dls, RNN4(len(vocab), 64, 2),
# CrossEntropyLossFlat() does the
# same thing as our loss_func
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
Even when we add more layers, we get a worse accuracy than our single-layer RNN:
learn = Learner(dls, RNN4(len(vocab), 64, 5),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
The reason is that we now have an even deeper model, which are more likely to lead to exploding or vanishing activations.
In practice, creating accurate models from multilayer RNNs are difficult because we're applying repeated matrix multiplication many, many times (each layer is another set of matrix multiplications). Multiplying by a number even a little greater than 1 will lead to exploding activations; and multiplying by a number even a little smaller than 1 will lead to vanishing activations.
We also have the problem of floating point numbers. Because of how they're stored on the computer, the numbers are more accurate the closer they are to 0. This inaccuracy leads to the vanishing gradients or exploding gradients problem, where in SGD, the weights are either not updated at all, or explode to infinity.
For RNNs, there're two types of layers that are commonly used to avoid exploding activations: gated recurrent units (GRUs) and long short-term memory (LSTM).
LSTM introduces another hidden state called the cell state that retains important information that happened earlier in the sentence (e.g., the subject's gender to predict "he/she/they"), that is, long short-term memory. The other hidden state is then like the sensory short-term memory.

So, LSTM looks like this:
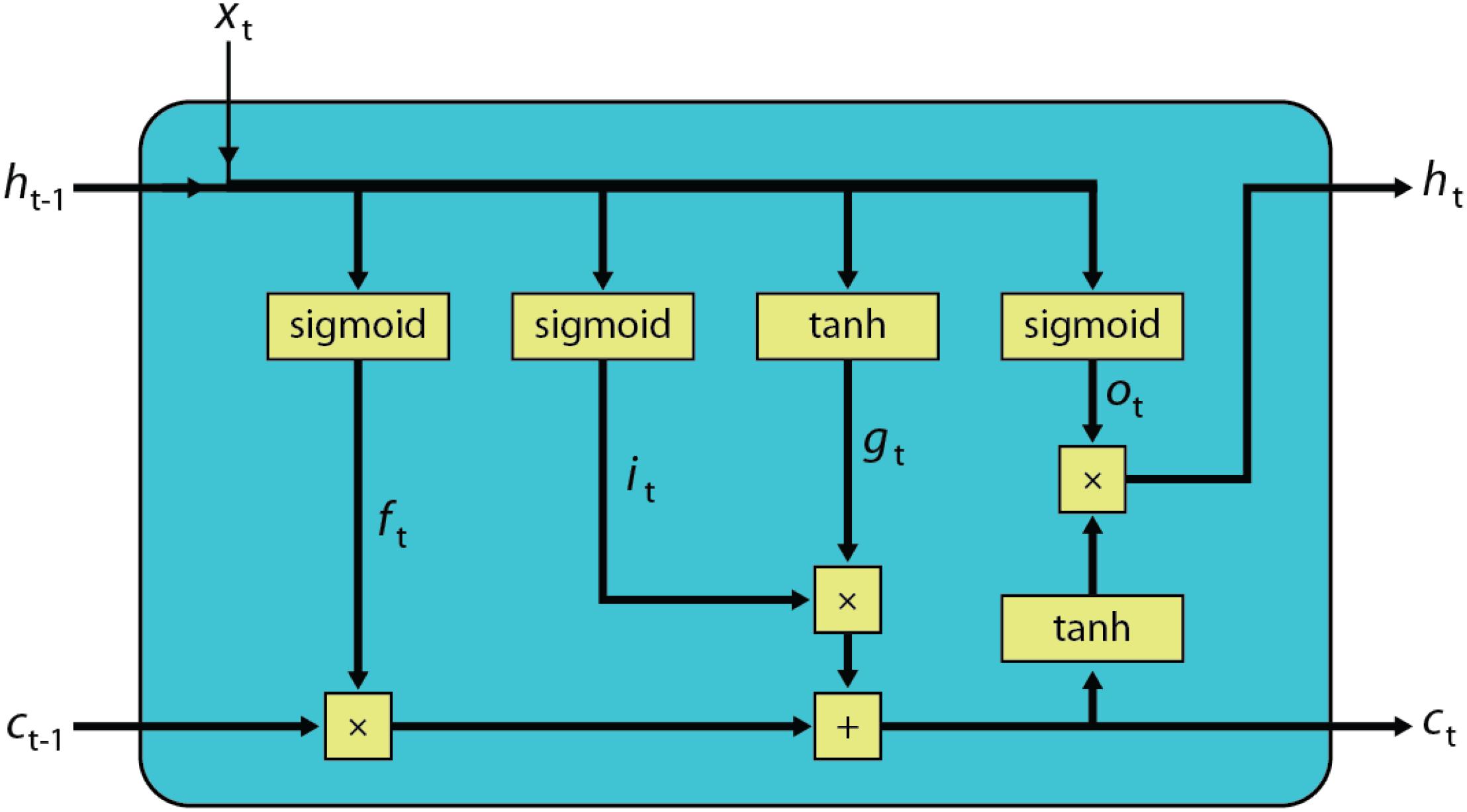
In essence, the blue box is our forward function, which uses the previous hidden states $h_{t-1}$ and $c_{t-1}$ and accepts an input batch $x_t$. The function updates the hidden states to yield $h_t$ and $c_t$, which become $h_{(t+1)-1}$ and $c_{(t+1)-1}$ for the next time step.
In LSTM, the hidden state $h_{t-1}$ and the input batch $x_t$ are concatenated instead of added like what we've been doing so far to create a tensor of size $h_{t-1}+x_t$. So, all the layers have an input size of $h_{t-1}+x_t$ and have an output size of $h_{t-1}$.
LSTM has four layers called gates. There's two different activation functions being used in LSTM: sigmoid (squishes to 0 to 1) and tanh (squishes to -1 to 1). From left to right:
- (1) Forget gate $f_t$: take what you currently know ($h_{t-1}$) and apply that to the input ($x_t$) to forget unimportant things in the cell state $c_{t-1}$.
- (2) Input gate $i_t$ and (3) cell gate $g_t$: these two gates work together, so I'll group them together and call them the remember gate. Basically, take what you currently know ($h_{t-1}$) and apply that to the input ($x_t$) to remember the important stuff from the cell gate $g_t$. Add the output from the remember gate to the cell state.
- (4) Output gate $o_t$: take important things from the new cell state that we might need for the next time step $t$.
The importance mentioned above is what's learned when we train the model at each time step (i.e. epoch).
The cell state $c_t$ is able to remember stuff much better (maintain a longer-term state) than the hidden state $h_t$ since it doesn't go through a single layer, hence avoiding vanishing and exploding activations.
In code:
class LSTM(Module):
def __init__(self, n_in, n_hid):
n_cat = n_in + n_hid
self.forget_gate = nn.Linear(n_cat, n_hid)
self.input_gate = nn.Linear(n_cat, n_hid)
self.cell_gate = nn.Linear(n_cat, n_hid)
self.output_gate = nn.Linear(n_cat, n_hid)
def forward(self, x, state):
h, c = state
h = torch.cat([h, x], dim=1)
f = torch.sigmoid(self.forget_gate(h))
c = c * f
i = torch.sigmoid(self.input_gate(h))
g = torch.tanh(self.cell_gate(h))
c = c + i * g
o = torch.sigmoid(self.output_gate(h))
h = o * torch.tanh(c)
return h, (h, c)
However, in practice, we refactor the code since it's inefficient to do four small matrix multiplications when we can do one big multiplication on the GPU in parallel. It's like typing with a single finger when you were given 10 (unless you're missing fingers). Also, since it takes time to concatenate the input $x_t$ and the hidden state $h_t$, we have two layers instead: one for the input and one for the hidden state. So:
class LSTM(Module):
def __init__(self, n_in, n_hid):
self.i_h = nn.Linear(n_in, 4 * n_hid)
self.h_h = nn.Linear(n_hid, 4 * n_hid)
def forward(self, x, state):
h, c = state
# .chunk(4, 1) splits the tensor into 4 tensors
# along the first dimension
gates = (self.i_h(x) + self.h_h(h).chunk(4, 1))
# It doesn't matter what order the gates are
# as long as we keep the order throughout
f, i, o = map(torch.sigmoid, gates[:3])
g = gates[3].tanh()
c = c * f + i * g
h = o * c.tanh()
return h, (h, c)
And, our LSTM is essentially what we already have through PyTorch's nn.LSTM. So, we can recreate our multilayer RNN:
bs = 64
class LSTM(Module):
def __init__(self, n_vocab, n_hidden, n_layers):
self.i_h = nn.Embedding(n_vocab, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.h_o = nn.Linear(n_hidden, n_vocab)
# We have two hidden states (h, c) that we'll keep together in state
self.state = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
h, state = self.rnn(self.i_h(x), self.state)
self.state = [s.detach() for s in state]
return self.h_o(h)
def reset(self):
for s in self.state: s.zero_()
learn = Learner(dls, LSTM(len(vocab), 64, 2),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 1e-2)
Although we reduced the chances of vanishing or exploding gradients, now we have a bit of overfitting. Although there aren't many data augmentation techniques for text (like translating to another language and then back to the original), we can apply regularization techniques like dropout, activation regularization, and temporal activation regularization.
For AWD-LSTM, we need to include 4 (5) things:
- Dropout: randomly (through a Bernoulli trial) remove some activations with probability $p$.
- Activation regularization: weight decay, but with activations instead of weights.
- Temporal activation regularization: activation regularization, but with the difference between two consecutive activations.
- Weight tying: tying the hidden to output weights with the input to hidden weights.
- (You also use non-monotically triggered average stochastic gradient descent (NT-ASGD) as the optimizer).
Dropout is where you randomly set some of the activations to zero during training to make sure all parameters are being useful in producing the output:
But, we can't just zero some activations without doing something else since we won't have the same scale when we take the sum of 5 activations compared to 2 activations. So, if we have $n$ activations and apply dropout with probability $p$, then we'll have on average $(1-p)n$ activations left. Finally, we can divide them by $1-p$ to rescale the remaining to $n$, which effectively applies dropout while maintaining the scale as if we still had all activations (making dropout act like an identity function).
The PyTorch implementation of dropout is as follows:
class Dropout(Module):
def __init__(self, p):
self.p = p
def forward(self, x):
# Only apply dropout during training
if self.training:
# Creates a mask with 1s at a probability of (1-p)
# and 0s at a probability of p
mask = x.new(*x.shape).bernoulli_(1 - self.p)
# Divide the mask in place by (1-p) and multiply with x
return x * mask.div_(1 - self.p)
# Don't apply dropout during inference
else:
return x
We apply dropout before passing the outputs of our LSTM layer to the final output layer.
To change the training attribute of a PyTorch Module, you can use the train method to set it to true and the eval method to set it to false. When you call these methods, it sets the training attribute for that Module and recursively applies it to the next Modules. You won't see it here often since it's applied automatically by fastai's Learner class.
Activation regularization (AR) and temporal activation regularization (TAR) are essentially weight decay, but with activations. With weight decay, we add a penalty to the loss (but in practice, we add to the gradient) to make the weights as small as possible to avoid overfitting (by making the loss have less steep points). For AR and TAR, we aim to make the final LSTM activations as small as possible.
With AR, we can do the following to the loss:
loss += alpha * activations.pow(2).mean()
But, we know from weight decay that it'll be more efficient to add them to the gradient instead of the loss:
grad += alpha * activations.mean()
Then, going straight to the gradient for TAR, we have:
grad += beta * (activation[:,1:] - activations[:,:-1]).mean()
We have two new hyperparameters that we can tune for AR and TAR: alpha and beta like how we could adjust wd for weight decay. To apply AR and TAR, we use the RNNRegularizer callback (although that class adds the square to the loss).
But, to make AR and TAR work, we need our new model to return three things: (1) the actual output, (2) the LSTM activations pre-dropout and (3) the LSTM activations post-dropout.
We apply AR on the post-dropout LSTM activations to not penalize the activations we dropped; and, we apply TAR on the pre-dropout LSTM activations because those dropped activations make a big difference between two consecutive time steps.
Finally, we have weight tying. Weight tying is used in language models because we go from our input vocab to some hidden state, then from the hidden state to our output, which are tokens from the same vocab. So, we can expect that the mappings from input to hidden will be the same for the mapping from hidden to output; that is, the mapping is invertible (or at least, try to enforce it to be invertible). Therefore, we can set the weights of the hidden to output layer to be equal to the weights of the input to hidden layer:
self.h_o.weight = self.i_h.weight
So, we now have our final model:
class AWDLSTM(Module):
def __init__(self, n_vocab, n_hidden, n_layers, p):
# What we had before in LSTM
self.i_h = nn.Embedding(n_vocab, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.h_o = nn.Linear(n_hidden, n_vocab)
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
# Dropout layer
self.drop = nn.Dropout(p)
# Weight tying
self.h_o.weight = self.i_h.weight
def forward(self, x):
h, state = self.rnn(self.i_h(x), self.h)
h_drop = self.drop(h)
self.h = [s.detach() for s in state]
return self.h_o(h_drop), h, h_drop
def reset(self):
for h in self.h: h.zero_()
Then, to train this model, we have:
learn = Learner(dls, AWDLSTM(len(vocab), 64, 2, 0.5),
loss_func=CrossEntropyLossFlat(), metrics=accuracy,
cbs=[ModelResetter, RNNRegularizer(alpha=2, beta=1)])
But, since we use those callbacks so often, we can instead use TextLearner which applies ModelResetter and RNNRegularizer (with alpha=2, beta=1 as defaults):
learn = TextLearner(dls, AWDLSTM(len(vocab), 64, 2, 0.5),
loss_func=CrossEntropyLossFlat(), metrics=accuracy)
Finally, when we train our model, we can also add weight decay for additional regularization:
learn.fit_one_cycle(15, 1e-2, wd=0.1)
And we've come a long ways from 49% accuracy with a single layer vanilla RNN.
So, a recurrent neural network is just a neural network that has some layers used repeatedly such that we can put them in a loop. A vanilla RNN is fairly difficult to get a good accuracy, and, when we attempt to do a vanilla multilayer RNN, it becomes even harder to get a good accuracy because of exploding and vanishing gradients. That's why we now have LSTM (but we can also use GRU, which has only one hidden state that splits during the time step into the hidden and cell states). However, LSTM has an issue of overfitting. So, what do we do when we overfit? We apply data augmentation techniques (since we might not have enough data), but there aren't many cheap and quick data augmentation techniques for text. Instead, we opt for regularization techniques like dropout, activation regularization, temporal activation regularization, and weight tying. Applying these regularization techniques creates a new kind of architecture that we could call a rudimentary AWD-LSTM.
For an actual AWD-LSTM, we have to apply dropout in a few more places:
- Embedding dropout: inside the embeddings, drop some random rows of embeddings.
- Input dropout: applied after the embedding layer.
- Weight dropout: appled to the weights of LSTM after each epoch.
- Hidden dropout: applied to the hidden state between two layers.
These additional regularizations (and averaged SGD) completes AWD-LSTM, where AWD-LSTM uses 5 different kinds of dropout (the 5th is the one where we drop some activations after LSTM). There are already good defaults set in place in fastai's implementation of AWD-LSTM that we used in this blog and we were able to adjust the magnitude of the dropouts with the drop_mult parameter.